個人情報を匿名化するプロセス：データ匿名化 第3回

こんにちは、株式会社ラクスで横断的にITエンジニアの育成や、技術推進、採用促進などを行っている開発管理課に所属している鈴木( @moomooya )です。

前回は匿名化された個人情報において個人が特定されないとはどういうことなのかについてお話ししました。

tech-blog.rakus.co.jp

今回は匿名化のプロセスについてどういった手順で行うのかをお話ししていこうと思います。

第1回、第2回がこってりした文量になってしまったので今回は軽めに行きたいと思います。

連載目次

• 『全文検索 〜 Elasticsearchとデータ匿名化手法』
• 『全文検索の探求 Elasticsearch(1) 』: プロジェクト方針およびElasticsearch概要
• 大量データを検索するサービスでElasticsearchはRDBの代替候補になりうるか？(Elasticsearch vs pg_bigm)』
• データ匿名化 第1回：匿名化された個人情報とは何なのか
• データ匿名化 第2回：個人情報は匿名化しても意味がないのではないか？
• データ匿名化 第3回：個人情報を匿名化するプロセス ←今読んでいる記事
• データ匿名化 第4回：匿名化のために行うデータ項目の一般化とは
• データ匿名化 第5回：データ匿名化の指標
• データ匿名化 第6回：実際の匿名化

匿名化の手順

データセットを匿名化する場合に以下の手順で進めて行きます。

1. 対象データセット内の識別子と準識別子を定義する
2. 識別子を削除する
3. 準識別子をなるべく秘匿せずに一般化する
4. 検証要件に合わせて一般化の度合いを調整する
5. 平均情報量を計測する

それぞれ見て行きましょう。

1. 対象データセット内の識別子と準識別子を定義する

まずはデータセットの各項目を識別子と準識別子に分けていきます。

• 識別子
  • その情報単体で個人を特定できる情報
  • 氏名、社員番号、会員番号、など
• 準識別子
  • 他の情報と容易に照合することができ、それにより特定の個人を識別することができることとなるもの
  • 性別、年齢、都道府県、居住ビル、など

2. 識別子を削除する

次に識別子をすべて削除します。削除は非可逆な置き換えを含みます。

3. 準識別子をなるべく秘匿せずに一般化する

秘匿、一般化という言葉が出てきました。

準識別子を匿名化する場合にはこんな方法があります。

• 秘匿
  • 外れ値などの特定しやすい値を（NULLなどで）上書きする
  • 上書きの単位は項目単位やレコード単位で行う
  • 秘匿されたデータの量は欠損としてメトリクス化される
    • 項目単位の欠損はセル欠損、レコード単位の欠損はレコード欠損と呼ばれる
• 一般化
  • 値をグルーピングした値に置き換えることで特定しにくい状態にする
    • 「1989年09月14日生まれ」を「1989年生まれ」にする、など
  • 一般化の前後で情報量を計測し、差分を求めることで失われた情報量を定量化する

秘匿してしまうとデータが完全に失われてしまうため、まずは出来るだけ一般化することができないかを検討すると良いでしょう。

サブサンプリング

データセットのレコード数が必要以上に多い場合は必要なレコード数を抽出（サンプリング）することで、データセットのサブセットを作ることも匿名化に有効な手段になります。

サブセットを作ることでデータセットに含まれているか、含まれていないかという情報を秘匿することができます。

一般化でグルーピングする範囲

一般化でグルーピングする範囲には注意が必要です。

例えば以下のような値の場合に単純に10ごとのグルーピングをすると実質的に一般化されていないことになります。

13才, 27才, 32才, 59才, 61才
  ↓
10代, 20代, 30代, 50代, 60代

このような場合は

0〜39才, 0〜39才, 0〜39才, 40〜79才, 40〜79才

といったようにグルーピングする値域を変えなければなりません。

ただし、大量のレコードを含むデータセットの場合には各値を見ながらグループの値域を判断するというのは現実的ではありません。Mondrianアルゴリズム*1というグループの値域をもとめるアルゴリズムがあるので、こちらを用いて値域を求めるのが良いでしょう。

4. 検証要件に合わせて一般化の観点や度合いを調整する

一般化は1度行って終わりではありません。 データセットの用途に応じて一般化の観点や度合いを調整する必要があります。どういうことかというと、

[リンゴ, レモン, キウイ, ニンジン, レタス, ダイコン, タンポポ, スズラン]

というデータセットを

[果物, 果物, 果物, 野菜, 野菜, 野菜, 花, 花]

と種類で一般化した場合に、検証したい内容が「種類で絞り込んだ検索性能」だったとしたら、一般化する観点を「種類」以外の観点に変えるべきでしょう。

一般化の観点が変われば情報量も変化することになります。変化した情報量が問題ないかどうかは匿名加工の方法を変更するたびに計測する必要があります。

5. 平均情報量（エントロピー）を計測する

平均情報量（エントロピー）とは

ここまでに何度か「情報量」という表現が出てきていますが、厳密には平均情報量（エントロピー）を扱い、確率の小ささの度合いを示します。

平均情報量の算出方法

例をあげると

赤玉4個、青玉2個、黄玉2個が入った袋から1個を取り出す時の平均情報量を求める時、それぞれの確率は

• 赤玉の確率 4/8 = 1/2
• 青玉の確率 2/8 = 1/4
• 黄玉の確率 2/8 = 1/4

となります。

情報量を求める公式は「」*2で、平均情報量は各場合の総和となります。

ちなみに分数の対数(log)は対数(log)の引き算に直せて、なので

$$ \begin{align} \log_2\frac{1}{\frac{2}{3}} &= \log_2{1} - \log_2{\frac{2}{3}} \\ &= 0 - \log_2{\frac{2}{3}} \\ &= -\log_2{\frac{2}{3}} \end{align} $$

とか

$$ \begin{align} \log_2\frac{1}{\frac{1}{2}} &= \log_2{1}-\log_2{\frac{1}{2}} \\ &= \log_2{1} - (\log_2{1} - \log_2{2}) \\ &= 0 - (0 - \log_2{2}) \\ &= \log_2{2} \end{align} $$

と変換できます。

先ほどの確率を公式に当てはめると

$$ \begin{align} \log_2\frac{1}{\frac{1}{2}} + \log_2\frac{1}{\frac{1}{4}} + \log_2\frac{1}{\frac{1}{4}} &= \log_2{2} + \log_2{4} + \log_2{4} \\ &= 5 bit \end{align} $$

となります。

今度は色を全て混ぜて（一般化して）灰玉8個から1つを選ぶ場合（当然常に灰玉が選ばれます）

$$ \begin{align} \log_2\frac{1}{\frac{8}{8}} &= \log_2\frac{1}{1} &= \log_2{1} \\ &= 0 bit \end{align} $$

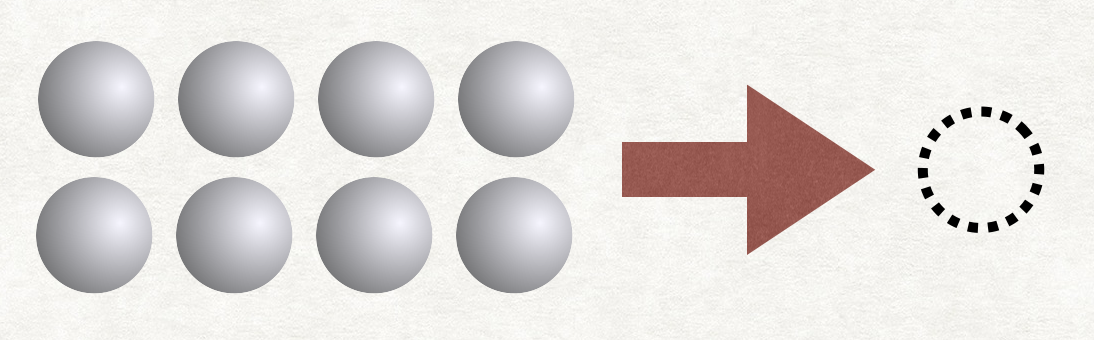
となり、情報量は0 bitとなります。この時、一般化によって情報量が5から0に損なわれていると考えます。

なお、情報量が損なわれる＝レコードが特定しにくくなるということなので、匿名加工後の情報量が大きければ大きいほどレコードを特定しやすいという見方ができます。ただし、これは情報量の多寡を比較することができますが、データセット自体の特性によって基準が変わるため「一律で情報量がいくつ以下であれば安全」という使い方はできないので勘違いしないでください。

具体的な例

[リンゴ, レモン, キウイ, ニンジン, レタス, ダイコン, タンポポ, スズラン]

といった値がバラバラなデータセットを「果物」「野菜」「花」と種類により一般化したとします。

[果物, 果物, 果物, 野菜, 野菜, 野菜, 花, 花]と一般化

この時の一般化前の情報量は

$$ \begin{align} 8 \times \log_2\frac{1}{\frac{1}{8}} &= 8 \times \log_2{8} \\ &= 24 bit \end{align} $$

一般化後の情報量は

$$ \begin{align} \log_2\frac{1}{\frac{3}{8}} + \log_2\frac{1}{\frac{3}{8}} + \log_2\frac{1}{\frac{1}{4}} &= -\log_2\frac{3}{8} - \log_2\frac{3}{8} + \log_2{4} \\ &= 4.83 bit \end{align} $$

*3

ここで一般化したデータが種類で一般化されたものでは検証に適さなかったため、色で別れるように一般化を見直したとします。

[赤, 赤, 黄, 黄, 緑, 緑, 白, 白]と一般化の観点を変更

その場合の情報量は

$$ \begin{align} 4 \times \log_2\frac{1}{\frac{1}{4}} &= 4 \times \log_2{4} \\ &= 8 bit \end{align} $$

となり、種類で一般化したデータセット（情報量 4.83 bit）よりも情報量が増しています。情報量が増している、すなわちレコードが特定しやすくなっているため、リスクマトリクスを再計測して匿名化度合いが十分かどうか再評価する必要がある、という考え方をします*4。

まとめ

今回はデータを匿名化するにあたっての手順と、匿名化したデータの情報量の算出について触れました。

これで異なる匿名化方法を選択したデータ同士を比較することができるようになりました。

---

次回は一般化の具体的なデータ置き換え例についてお話させていただければと思います。

連載目次

• 『全文検索 〜 Elasticsearchとデータ匿名化手法』
• 『全文検索の探求 Elasticsearch(1) 』: プロジェクト方針およびElasticsearch概要
• 大量データを検索するサービスでElasticsearchはRDBの代替候補になりうるか？(Elasticsearch vs pg_bigm)』
• データ匿名化 第1回：匿名化された個人情報とは何なのか
• データ匿名化 第2回：個人情報は匿名化しても意味がないのではないか？
• データ匿名化 第3回：個人情報を匿名化するプロセス ←今読んでいる記事
• データ匿名化 第4回：匿名化のために行うデータ項目の一般化とは
• データ匿名化 第5回：データ匿名化の指標
• データ匿名化 第6回：実際の匿名化

*1:名前の由来はコンポジションシリーズで有名な画家ピエト・モンドリアンかと。

*2:ちなみに対数の底は2に限らないようですが、底が2の場合に単位をbitとするようなので本稿では2を用います。

*3:対数の計算はGoogle計算機やExcelや関数電卓で計算してしまうのが楽です。

*4:情報量が増す≠特定されるのでダメ、ではありません。情報量が増した場合にはその情報量が「問題あるのかないのか」を再測定する必要があるという考え方をしましょう。